Simulation
Contents
Simulation#
In this page we will simulate 100 individuals and create the discrete probabilities. I will plot some graph using the data.
Warning
Remember that dhr.func is the sintax that calls the file with the functions see before.
Packages#
import numpy as np
import pandas as pd
import dhr_functions as dhr
Using the model solution#
Before simulating the data and the probabilities, I will run the model solution
probs_w, _, _, _, _, vf = dhr.model_solution()
Simulation#
Parameters#
We need some parameters to run our simulation:
Number of simulation
μ (value of leisure)
Non pecuniary cost
Total days in the month
Shock mean
Shock standart deviation
Seed to save the random results
sim_nb = 100
mu = 4
P = 3
Tm = 30
eps_mean = 0
eps_sd = 1
np.random.seed(1996)
Creating Matrices#
Now I will create the matrices to store the simulation results. Each colum stores the individual simulated data for all the years
# Store leisure decision
L_dec = np.empty((Tm,sim_nb))
L_dec[:] = np.nan
# Store days worked until t
d_dec = np.empty((Tm,sim_nb))
d_dec[:] = np.nan
# Store days worked in t + 1
d1_dec = np.empty((Tm,sim_nb))
d1_dec[:] = np.nan
# Store ϵ received in t
e_dec = np.empty((Tm,sim_nb))
e_dec[:] = np.nan
# Utility gain from optimal choice
u_dec = np.empty((Tm,sim_nb))
u_dec[:] = np.nan
Simulating the individuals#
We will simulated our indiviuals follow these steps:
Draw the shock
Compute the value for working and leisure
Pick the max
Store the data
for s in range(sim_nb):
# Every individual starts with no days worked
d = 0
for t in range(30):
# Store days worked until t
d_dec[t,s] = d
# Need condition for last period
if t != 29:
# 1. Draw shock
e_shock = np.random.normal(loc = eps_mean, scale = eps_sd)
# 2. Compute values for decisions: Using Value function from model solution
w = vf[t+1,d+1]
l = e_shock + mu - P + vf[t+1,d]
# 3. Pick optmal choice
dec = max(w,l)
u = dec
if dec == w:
dec = 0
else:
dec = 1
if dec == 0:
d += 1
else:
pass
else:
# 1. Draw shock
e_shock = np.random.normal(eps_mean, eps_sd)
# 2. Compute values for decisions
w = dhr.income_g(t, d+1)
l = e_shock + dhr.income_g(t, d)
# 3. Pick optmal choice
dec = max(w,l)
u = dec
if dec == w:
dec = 0
else:
dec = 1
if dec == 0:
d += 1
else:
pass
# 4. Store results
L_dec[t,s] = dec
d1_dec[t,s] = d
e_dec[t,s] = e_shock
u_dec[t,s] = u
Now we will create a dataframe using the simulated matrices
simulated_data = []
for i in range(sim_nb):
s = {}
s['id'] = i
s['t'] = list(range(1,31))
s['d+1'] = list(d1_dec[:,i])
s['d'] = list(d_dec[:,i])
s['L'] = list(L_dec[:,i])
s['eps'] = list(e_dec[:,i])
s['U'] = list(u_dec[:,i])
s = pd.DataFrame(s)
simulated_data.append(s)
simulated_data = pd.concat(simulated_data, axis = 0).reset_index().drop('index', axis = 1)
Discrete probabilities#
Using the model solution, we can create the discrete probabilities matrix for the days worked. First, create a matrix to store the results.
prob_sim = np.zeros((Tm,Tm))
We will start with every individual in the same position, wich means a mass of 1 in t = 0 and d = 0
prob_sim[0,0] = 1 #P(t = 1, d = 0)
To compute the discrete probability matrix, we will use two things:
The probability of working in t conditional on d (from the model solution)
The mass of teachers in t-1 and with an specific value of d
for t in range(1,Tm):
for d in range(t):
prob_mass = prob_sim[t-1,d] # Mass of teacher in t = t-1, d = d
prob_w_t_d = probs_w[t-1,d] # P(L = 0 | t = t-1, d = d)
if np.isnan(prob_w_t_d): # Maybe is not possible, but I defined as nan in the model solution
prob_w_t_d = 0
else:
pass
prob_sim[t,d] = prob_sim[t,d] + (1-prob_w_t_d)*prob_mass # Adding the 0 to the teachers proportion multiplied by the conditional prob to leisure
prob_sim[t,d+1] = prob_sim[t,d+1] + prob_w_t_d*prob_mass # Same as (214) but now with prob to work
Functions#
The simulation and the discrete probabilities are also included in the functions file
_, L_dec, d_dec, d1_dec, e_dec, u_dec, _= dhr.simulate_data()
L_dec
array([[0., 0., 1., ..., 0., 1., 0.],
[0., 0., 0., ..., 1., 0., 1.],
[1., 0., 0., ..., 0., 0., 1.],
...,
[1., 0., 0., ..., 1., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]])
The probability function
prob_sim = dhr.discrete_probs()
prob_sim
array([[1.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[3.10539517e-01, 6.89460483e-01, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[9.74900563e-02, 4.26097965e-01, 4.76411979e-01, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[3.14817833e-02, 1.98020433e-01, 4.41128340e-01, 3.29369444e-01,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[1.08830020e-02, 8.23818867e-02, 2.72472778e-01, 4.06523682e-01,
2.27738652e-01, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[4.32965468e-03, 3.27384767e-02, 1.40485684e-01, 3.13638823e-01,
3.51335800e-01, 1.57471563e-01, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[2.14188900e-03, 1.30910032e-02, 6.54905564e-02, 1.93657518e-01,
3.25216996e-01, 2.91516520e-01, 1.08885517e-01, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[1.33253009e-03, 5.65089524e-03, 2.88472208e-02, 1.04741620e-01,
2.34163399e-01, 3.14806919e-01, 2.35167186e-01, 7.52902289e-02,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[9.74783398e-04, 2.87883245e-03, 1.24903214e-02, 5.19490940e-02,
1.44553613e-01, 2.59021331e-01, 2.90232632e-01, 1.85839027e-01,
5.20603651e-02, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[7.75226687e-04, 1.82603897e-03, 5.61942476e-03, 2.43485918e-02,
8.03688594e-02, 1.79832278e-01, 2.68645643e-01, 2.58022875e-01,
1.44563275e-01, 3.59977881e-02, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[6.38694586e-04, 1.39384847e-03, 2.85243715e-03, 1.10975903e-02,
4.14526120e-02, 1.10999687e-01, 2.07223959e-01, 2.65367033e-01,
2.23016273e-01, 1.11066745e-01, 2.48911191e-02, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[5.33342519e-04, 1.18264017e-03, 1.76748043e-03, 5.12521654e-03,
2.02617449e-02, 6.28327032e-02, 1.40670666e-01, 2.25160900e-01,
2.52300065e-01, 1.88475636e-01, 8.44783298e-02, 1.72112745e-02,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[4.47550768e-04, 1.04912475e-03, 1.34544767e-03, 2.56762097e-03,
9.58156291e-03, 3.32977203e-02, 8.68212827e-02, 1.66734516e-01,
2.33533929e-01, 2.32607814e-01, 1.56388563e-01, 6.37239181e-02,
1.19009502e-02, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[3.76209203e-04, 9.43792709e-04, 1.17508030e-03, 1.52220268e-03,
4.51531817e-03, 1.67801702e-02, 4.97727466e-02, 1.11469620e-01,
1.87343723e-01, 2.33248135e-01, 2.09091313e-01, 1.27798042e-01,
4.77345871e-02, 8.22906034e-03, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[3.16429117e-04, 8.50627366e-04, 1.09389513e-03, 1.11757663e-03,
2.23473674e-03, 8.16353267e-03, 2.69072772e-02, 6.87959366e-02,
1.34877835e-01, 2.01506826e-01, 2.25794845e-01, 1.84009287e-01,
1.03095460e-01, 3.55456491e-02, 5.69008632e-03, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[2.66201740e-04, 7.64927002e-04, 1.03986882e-03, 9.74255066e-04,
1.26057401e-03, 3.91527448e-03, 1.38799743e-02, 3.98126456e-02,
8.91814643e-02, 1.55435091e-01, 2.09000582e-01, 2.12902432e-01,
1.59044334e-01, 8.22538079e-02, 2.63340873e-02, 3.93448109e-03,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[2.23961565e-04, 6.85527837e-04, 9.91106189e-04, 9.31133039e-04,
8.72496559e-04, 1.92341723e-03, 6.90858783e-03, 2.18545281e-02,
5.50394007e-02, 1.09622611e-01, 1.71962031e-01, 2.10204449e-01,
1.96285187e-01, 1.35351574e-01, 6.50004749e-02, 1.94229679e-02,
2.72054598e-03, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[1.88427622e-04, 6.12224435e-04, 9.40993342e-04, 9.21067096e-04,
7.38240977e-04, 1.03668648e-03, 3.36703760e-03, 1.14841160e-02,
3.20848393e-02, 7.18792736e-02, 1.28856606e-01, 1.83761252e-01,
2.05909834e-01, 1.77484880e-01, 1.13645619e-01, 5.09381031e-02,
1.42696438e-02, 1.88115542e-03, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[1.58532363e-04, 5.44969210e-04, 8.88349568e-04, 9.17429722e-04,
7.09400101e-04, 6.68382542e-04, 1.65027905e-03, 5.82532857e-03,
1.78275580e-02, 4.43609785e-02, 8.94587988e-02, 1.45796750e-01,
1.90594921e-01, 1.97139669e-01, 1.57788072e-01, 9.42979965e-02,
3.96245069e-02, 1.04473301e-02, 1.30074836e-03, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[1.33380340e-04, 4.83655417e-04, 8.33741734e-04, 9.10605580e-04,
7.20326215e-04, 5.35396157e-04, 8.57521618e-04, 2.88158788e-03,
9.51041560e-03, 2.60108670e-02, 5.82751078e-02, 1.06841172e-01,
1.59618668e-01, 1.92614221e-01, 1.84998224e-01, 1.38199000e-01,
7.74291726e-02, 3.06222526e-02, 7.62526625e-03, 8.99418659e-04,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[1.12218846e-04, 4.28081898e-04, 7.78169588e-04, 8.97757995e-04,
7.42631332e-04, 5.06287477e-04, 5.13927832e-04, 1.41494749e-03,
4.90216490e-03, 1.45962305e-02, 3.59651380e-02, 7.32595616e-02,
1.23125010e-01, 1.69799035e-01, 1.90264400e-01, 1.70558906e-01,
1.19449227e-01, 6.29874807e-02, 2.35268190e-02, 5.55008979e-03,
6.21914240e-04, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[9.44147367e-05, 3.77968520e-04, 7.22621351e-04, 8.78619286e-04,
7.64669319e-04, 5.20718333e-04, 3.81879446e-04, 7.15866572e-04,
2.45856364e-03, 7.88518496e-03, 2.11885069e-02, 4.74718676e-02,
8.86449244e-02, 1.37525699e-01, 1.76113368e-01, 1.84184516e-01,
1.54789652e-01, 1.02028659e-01, 5.08123853e-02, 1.79803232e-02,
4.02956263e-03, 4.30030351e-04, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[7.94353427e-05, 3.32981222e-04, 6.67939880e-04, 8.53837219e-04,
7.82017791e-04, 5.51069787e-04, 3.47405129e-04, 4.00830898e-04,
1.21299629e-03, 4.12114275e-03, 1.19882996e-02, 2.92979103e-02,
6.01753012e-02, 1.03726478e-01, 1.49431443e-01, 1.78603620e-01,
1.75115097e-01, 1.38510905e-01, 8.62265158e-02, 4.06824616e-02,
1.36759899e-02, 2.91897180e-03, 2.97349845e-04, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[6.68325082e-05, 2.92754836e-04, 6.14796929e-04, 8.24339996e-04,
7.93250414e-04, 5.85051932e-04, 3.56876089e-04, 2.72244172e-04,
6.02743762e-04, 2.09362088e-03, 6.54598525e-03, 1.73289643e-02,
3.88247445e-02, 7.36124742e-02, 1.17828176e-01, 1.58432155e-01,
1.77527280e-01, 1.63821329e-01, 1.22379208e-01, 7.21744654e-02,
3.23499513e-02, 1.03570460e-02, 2.11010302e-03, 2.05606256e-04,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[5.62291796e-05, 2.56911072e-04, 5.63703259e-04, 7.91094888e-04,
7.98161664e-04, 6.17408843e-04, 3.84850273e-04, 2.32582094e-04,
3.17916286e-04, 1.04005294e-03, 3.46328320e-03, 9.87293907e-03,
2.39612194e-02, 4.95580650e-02, 8.72546779e-02, 1.30356028e-01,
1.64323718e-01, 1.73298480e-01, 1.51034879e-01, 1.06889160e-01,
5.98871079e-02, 2.55643144e-02, 7.81255451e-03, 1.52249427e-03,
1.42169008e-04, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[4.73081249e-05, 2.25071835e-04, 5.15029067e-04, 7.55018011e-04,
7.97040483e-04, 6.45981878e-04, 4.19334622e-04, 2.35002898e-04,
1.95287343e-04, 5.11168434e-04, 1.78122067e-03, 5.44090264e-03,
1.42197024e-02, 3.18588072e-02, 6.11888852e-02, 1.00553062e-01,
1.40836335e-01, 1.67092769e-01, 1.66429323e-01, 1.37414268e-01,
9.23872628e-02, 4.92972377e-02, 2.00872301e-02, 5.87183481e-03,
1.09661211e-03, 9.83045319e-05, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[3.98024423e-05, 1.96868689e-04, 4.69025829e-04, 7.16942504e-04,
7.90373397e-04, 6.69948119e-04, 4.54847362e-04, 2.56748178e-04,
1.52370609e-04, 2.55970625e-04, 8.92918383e-04, 2.91036994e-03,
8.14949192e-03, 1.96620284e-02, 4.09082372e-02, 7.33342115e-02,
1.12981964e-01, 1.48937431e-01, 1.66888071e-01, 1.57477089e-01,
1.23521747e-01, 7.90923725e-02, 4.02848538e-02, 1.57012470e-02,
4.39849935e-03, 7.88596749e-04, 6.79738936e-05, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00],
[3.34875757e-05, 1.71949304e-04, 4.25846669e-04, 6.77609221e-04,
7.78723200e-04, 6.89054222e-04, 4.88974228e-04, 2.86472375e-04,
1.48850998e-04, 1.40259962e-04, 4.37168841e-04, 1.51537792e-03,
4.52683574e-03, 1.17015416e-02, 2.62172814e-02, 5.09128675e-02,
8.55670315e-02, 1.24075575e-01, 1.54475877e-01, 1.63984430e-01,
1.47000592e-01, 1.09813617e-01, 6.71187962e-02, 3.26998883e-02,
1.22139251e-02, 3.28470889e-03, 5.66257547e-04, 4.70013958e-05,
0.00000000e+00, 0.00000000e+00],
[2.81745959e-05, 1.49981623e-04, 3.85564518e-04, 6.37665769e-04,
7.62680936e-04, 7.03280677e-04, 5.20717970e-04, 3.18600358e-04,
1.64789954e-04, 9.53476288e-05, 2.09306723e-04, 7.69836817e-04,
2.44452570e-03, 6.74050182e-03, 1.61801922e-02, 3.38367967e-02,
6.16049780e-02, 9.74483628e-02, 1.33455209e-01, 1.57409622e-01,
1.58744278e-01, 1.35527014e-01, 9.66406620e-02, 5.64992711e-02,
2.63791996e-02, 9.45892670e-03, 2.44596460e-03, 4.06047532e-04,
3.24997008e-05, 0.00000000e+00],
[2.37045482e-05, 1.30656298e-04, 3.48188054e-04, 5.97668581e-04,
7.42846623e-04, 7.12704840e-04, 5.49682503e-04, 3.50667379e-04,
1.89192783e-04, 8.81277590e-05, 9.79436430e-05, 3.82251298e-04,
1.28654120e-03, 3.76999560e-03, 9.65300066e-03, 2.16279175e-02,
4.24043230e-02, 7.26640077e-02, 1.08557827e-01, 1.40846045e-01,
1.57821414e-01, 1.51580881e-01, 1.23529115e-01, 8.42555360e-02,
4.72060984e-02, 2.11586603e-02, 7.29516463e-03, 1.81657361e-03,
2.90794004e-04, 2.24723231e-05]])
Plots#
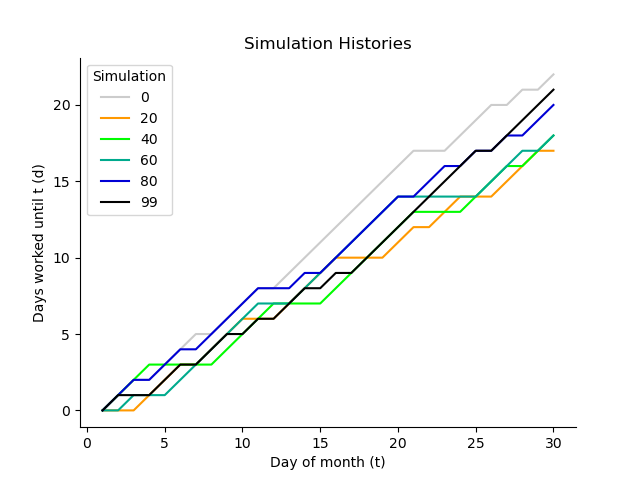
Plotting histories simulated#
dhr.simulation_plot()
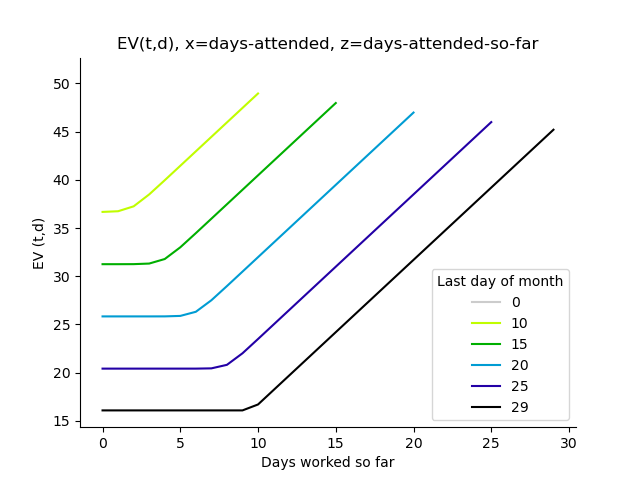
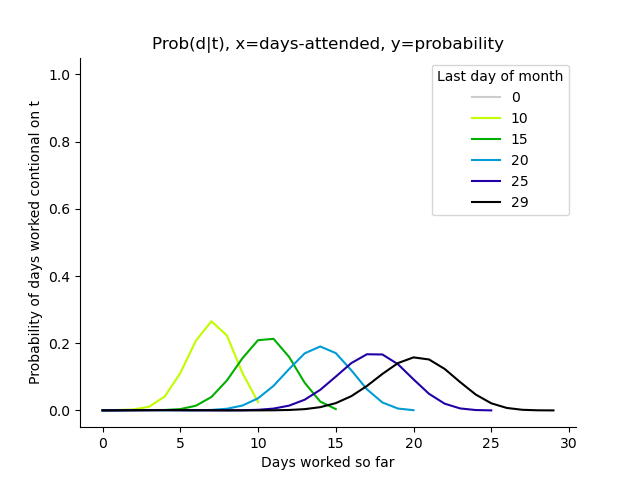
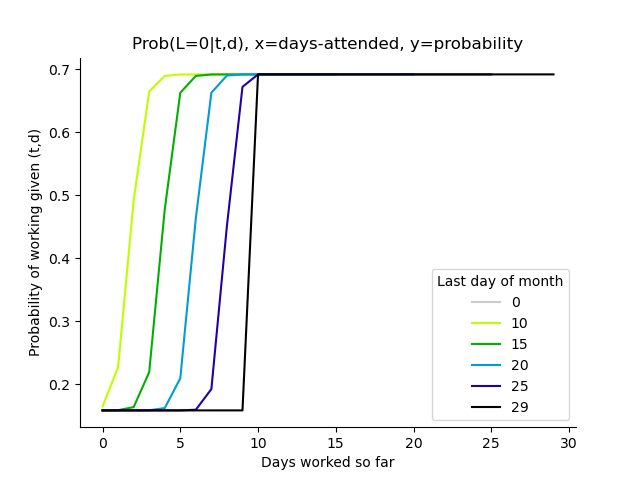
Plotting probability of working, probability of days worked and EVs#
dhr.t_graphs()